
Naive Bayes algorithms are mostly used in text classification tasks like sentiment analysis, spam filtering, recommendation systems etc. due to their higher success rate over other machine learning algorithms. They are easy to implement and can be used for realtime inference. This blog covers basic concepts of Naive Bayes Classifier algorithm and its application to sentence classification. Specifically, we will look at implementation of Naive Bayes Text Classifier using python for Ford Sentence Classification Dataset (Kaggle) [1] from scratch (without using libraries).
This section provides a brief explanation of the Naive Bayes algorithm and the Ford Sentence Dataset that is used in this blog.
Bayes’ Theorem provides a way to calculate the probability of a piece of data belonging to a given class, given our prior knowledge. Bayes’ Theorem is stated as:
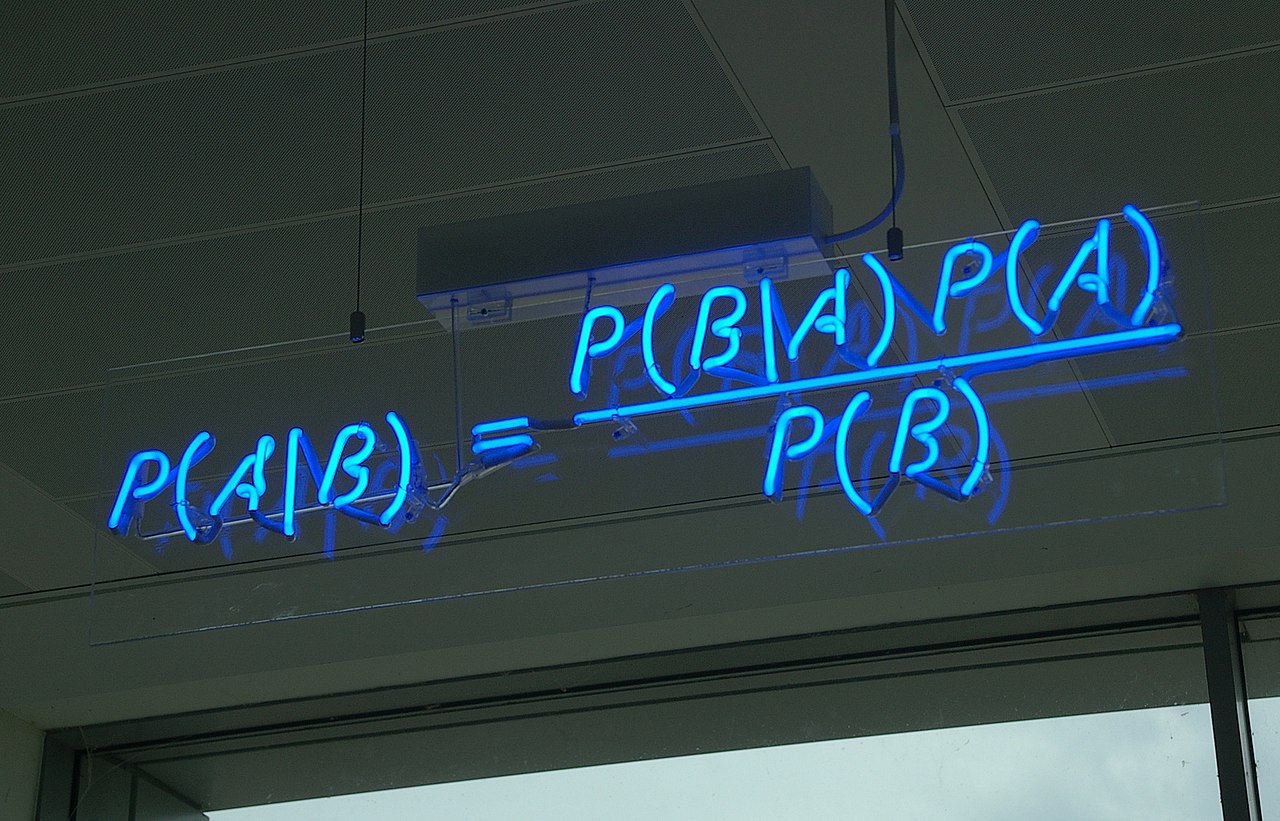
Where P(A|B) = Probability that A will happen given Evidence B has already happened
P(B|A) = Probability that B will happen given Evidence A has already happened
P(A) = Probability that A will happen
P(B) = Probability that B will happen
Naive Bayes classifier is a machine learning classification algorithm based on Bayes Theorem. Naive Bayes classification algorithm assumes that the given features are independent of each other. In most of the real life cases, the predictors are dependent, this hinders the performance of the classifier.
P(class | x1, x2, …, xn) = P(x1, x2, …, xn | class) * P(class) / P(x1, x2, …, xn)
Where P(class| x1, x2, …, xn ) = Posterior probability of class given data
P(x1, x2, …, xn |class) = Conditional probability of data given class
P(class) = Prioir probability of class
P(x1, x2, …, xn ) = Probability of data
Now, if any two events A and B are independent, then,
P(A,B) = P(A)P(B)
Lets apply this independence assumption to the bayes theorem in the context of Naive Bayes classification algorithm.
P(class | x1, x2, …, xn) = P(x1|class) * P(x2|class) * ....... * P(xn|class) * P(class) / P(x1, x2, …, xn)
This blog uses Ford Sentence Classification Dataset from kaggle (Ford Sentence Classification Dataset).
This is a preprocessed dataset for the Ford Business Solutions Hiring Challenge @ HackerEarth aimed at enabling CRM-based companies to help with their downstream services which play a vital role in deciding the skill score and fit score of candidates.
Data files:
1. train_data.csv - Training samples of sentences and corresponding class labels
2. test_data.csv - Unlabeled test data
3. sample_submission.csv - Sample submission test file for the competition
The following are the sentence classes in the training data
1. Education
2. Experience
3. Requirement
4. Responsibility
5. Skill
6. SoftSkill
The main goal of this blog is to build a sentence classifier using Naive Bayes classification algorithm on Ford Sentence Classification Dataset.
Data Download:
Download the dataset from Ford Sentence Classification Dataset (Kaggle) . Extr act th e downloaded archive.zip folder which contains sample_submission.csv, train_data.csv and test_data.csv. P lace the extracted data files in the working directory.
Import the required packages

Load .csv files using pandas, drop unnecessary columns and drop rows containing NaN. Rename column names

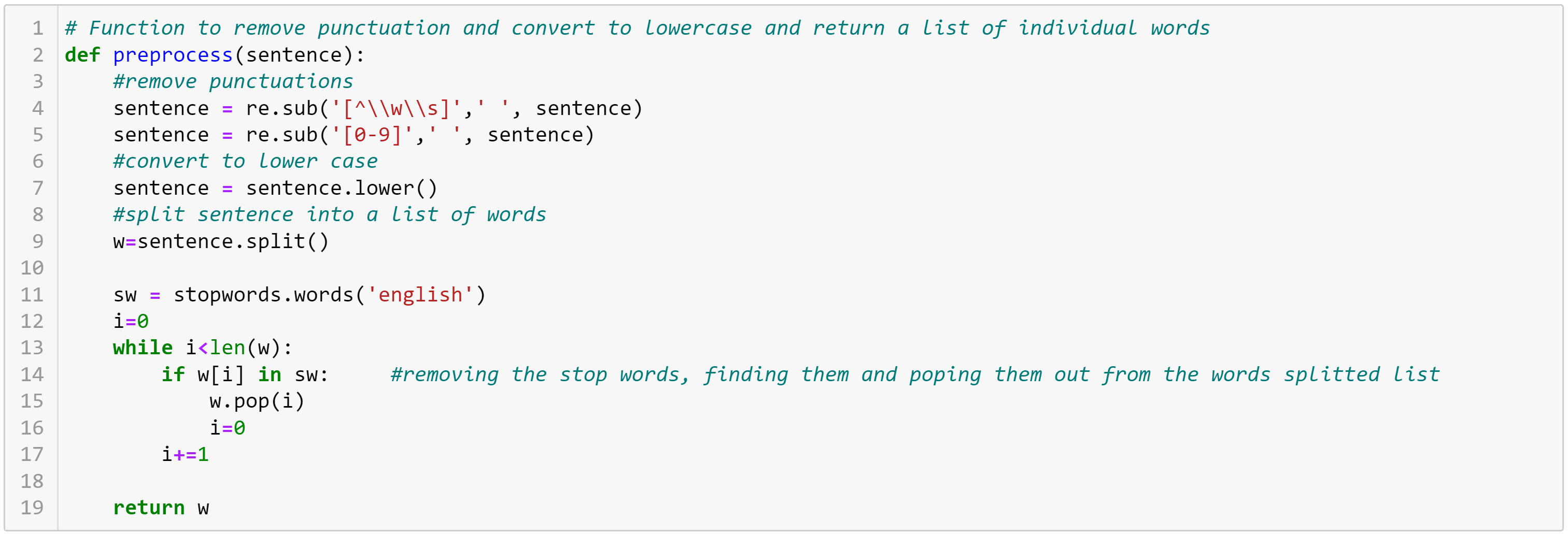
Perform preprocessing of sentences to remove noisy words and punctuation. Let's write a function that can perform required preprocessing steps like
1. Remove special punctuation characters from text sentences
2. Remove unnecessary stop words like "an","the" etc. from the sentence using list of stop words from nltk library
3. Remove numbers and convert to lower case
4. Split sentence to form list of words
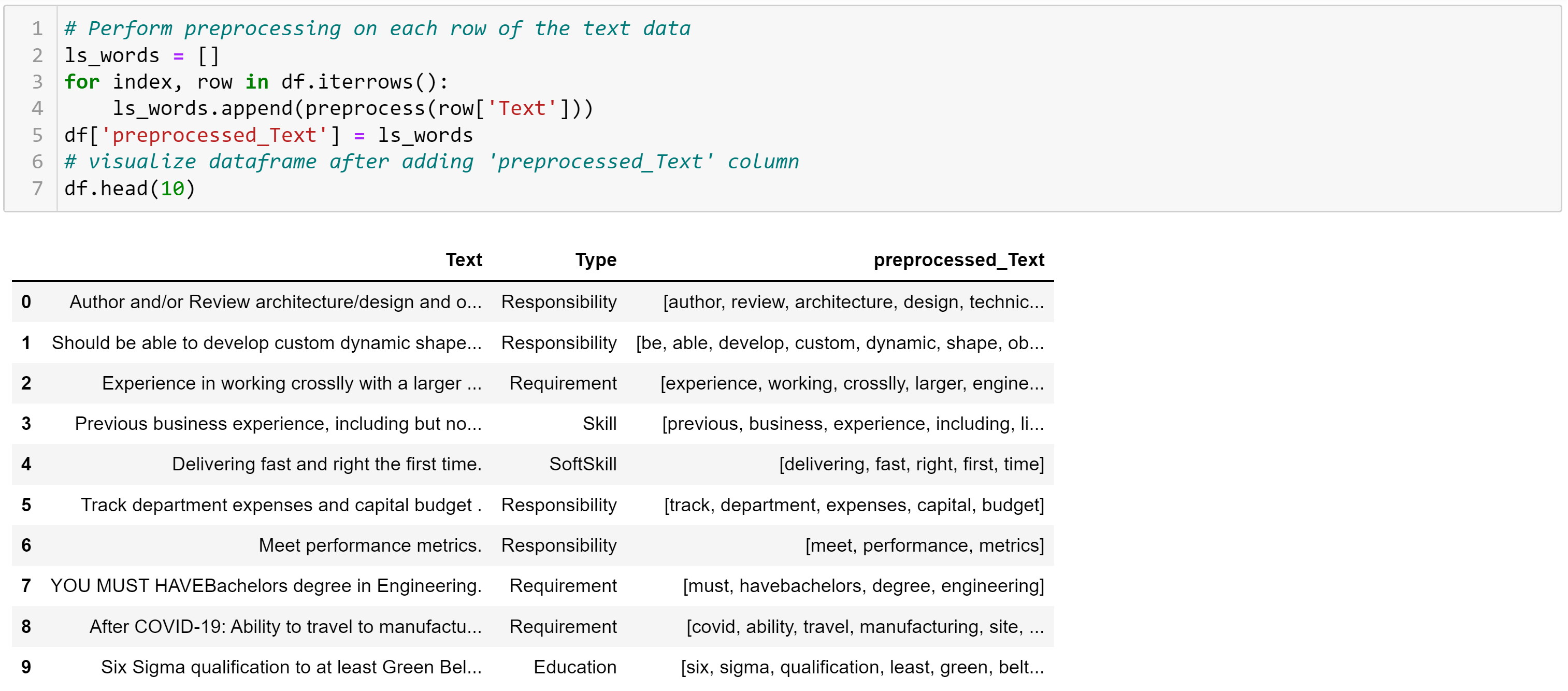
Apply preprocessing function to each of the sentence in the dataframe and add the result to a new column.
Here 'Text' column is the original raw text data, and the column, 'preprocessed_Text' is the preprocessed text added as new column to our dataframe.
Data Partitioning:

This step can be performed in two stages,
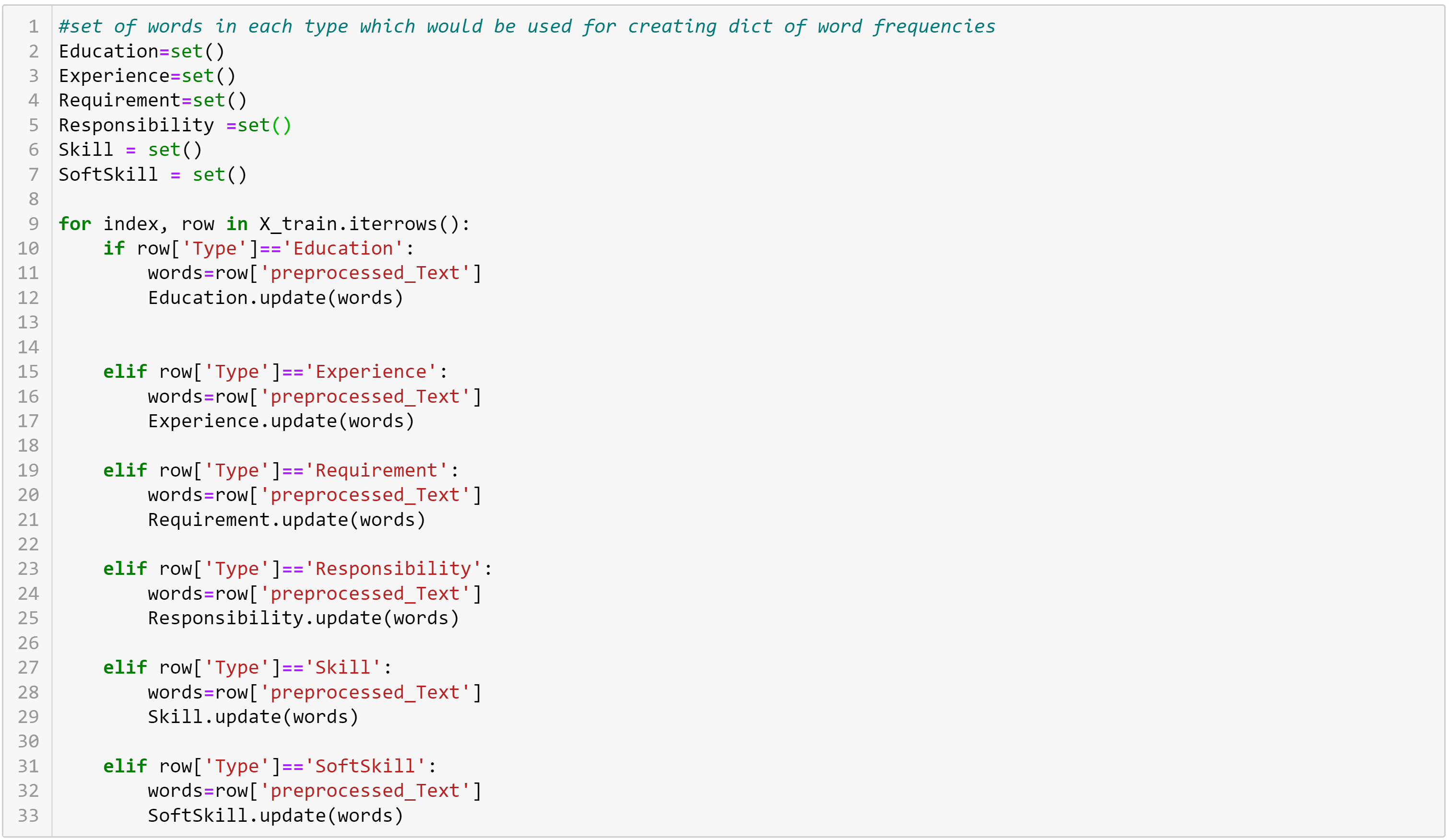
1. Identify unique words in each class
2. Counting the frequency of occurence of each word in every class
We are using data type set() for storing words as it is going to be easy for computation of unique values and perform set operations.
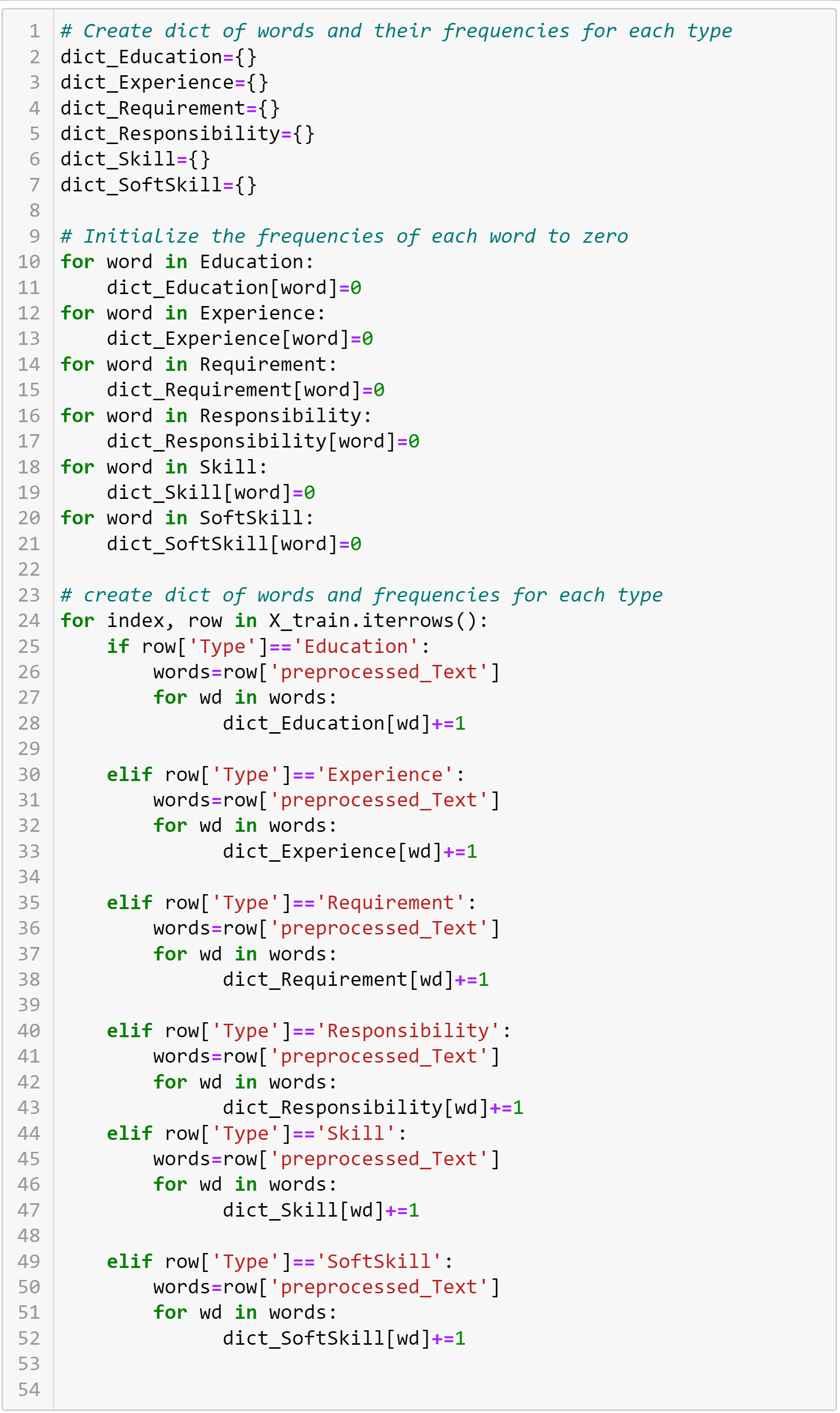
Initialize each class unique words as empty set and iteratively add unique words to each class set using a for loop by parsing through rows of all sentences in the training data.
For this step, we use datatype 'dictionary' , which will enable us to use key value pairs for storing word and the corresponding frequency. Create empty dictionary for each class and append the frequency of occurence of each word for each class using a for loop going through all the unique words in each class.

This portion of code is written as a part of user defined function, NBC(add_one_smoothing=False, X= X_val, Y = y_val, a= 0.1)
where X = Input features from either val or test set
Y = labels for val or test set
a = alpha in laplace smoothing
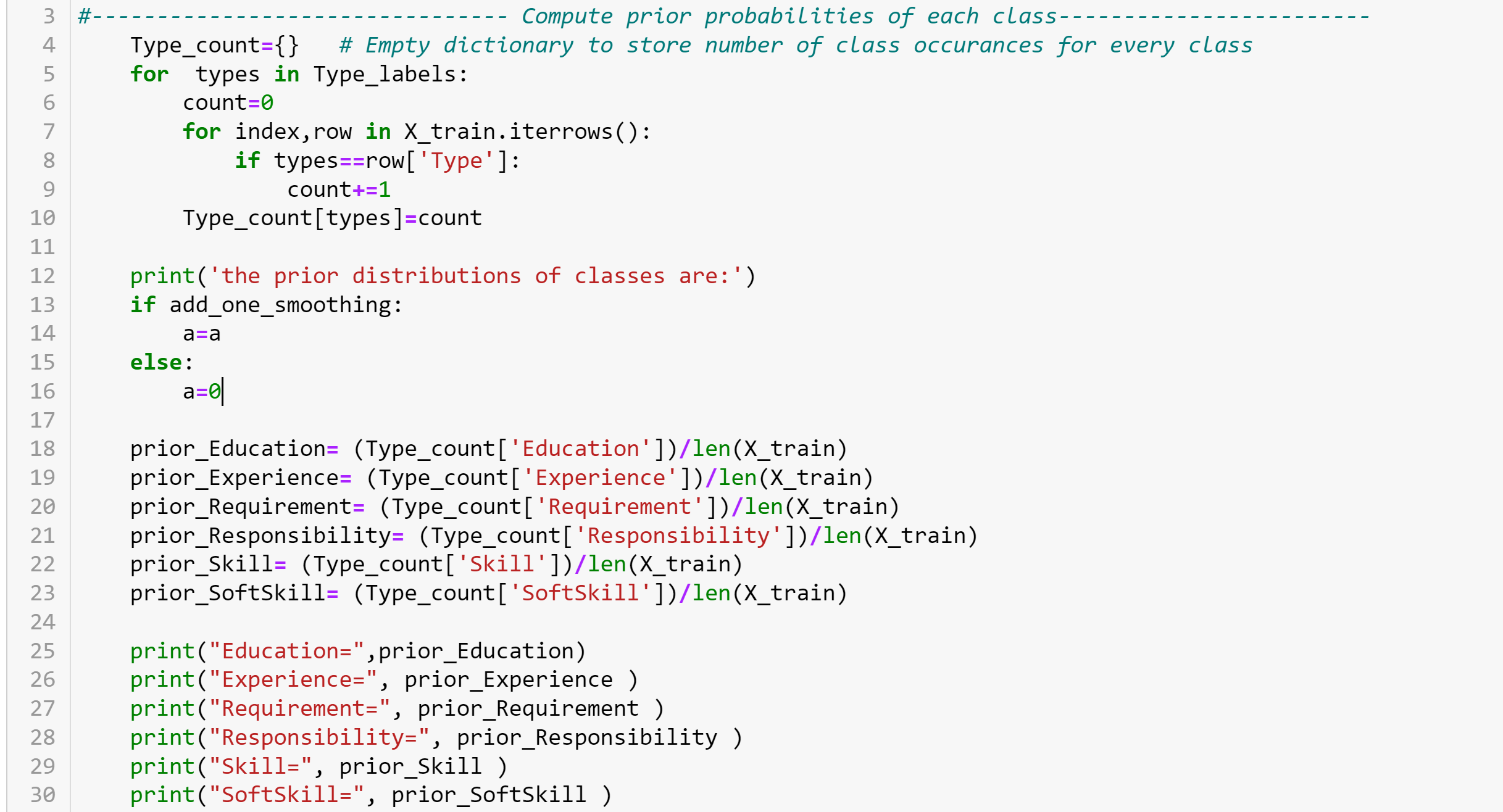
We can compute the prior probability of each class P(class) using
P(class) = [no. of times the class occurs/total no. of datapoints]
We can compute the class conditional probabilities given words as a product of individual probabilities of words assuming independence
Class conditional probability = P(x1|class) * P(x2|class) * ....... * P(xn|class)
The probability of word given each class is given by,
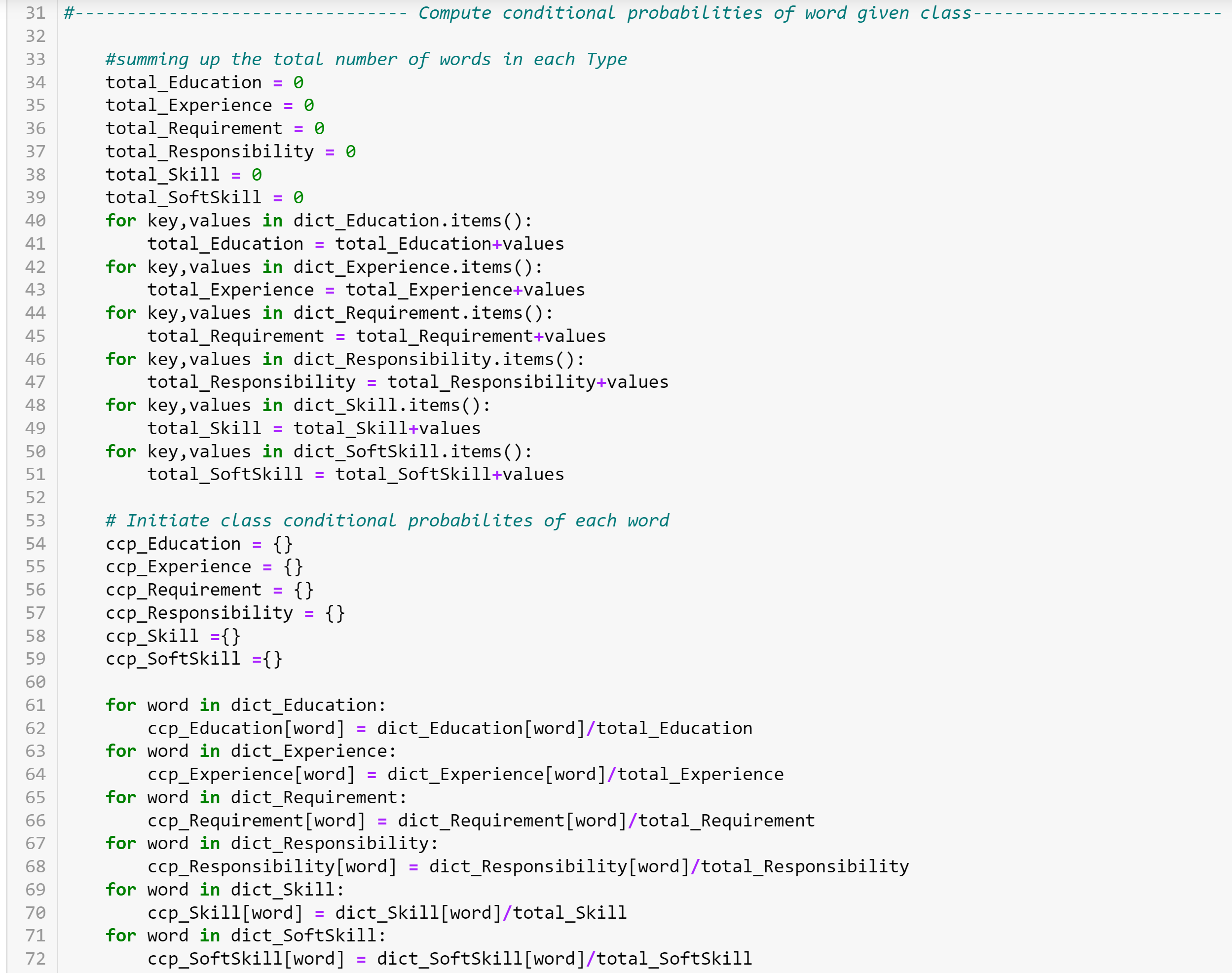
P(word/class) = [freq of word in given class/no. of total words in the given class]
The following code computes class conditional probabilities of each word in a given class by computing the ratio of freq of occurance of word in given class to the total no. of words in each class. Class conditional probabilities for each class are stored in dictionary with word and its conditional probability as key value pairs respectively.
In some cases when we encounter a new word in test, we would end up with 'zero frequency' problem where individual class conditional probabilities would become 'zero' (0). To address this we use Add-one (Laplace) smoothing as a reguralizer. Laplace smoothing is a simple smoothing technique that Add 1 to the count of all classes in the training set before normalizing into probabilities. We can adjust the strength of smoothing with hyperparameter 'alpha' or 'a'
Here we are adding class conditional probabilities for words in each class to have atleast one occurance of word in every class (K=Number of dimensions in given sample, a = hyperparameter to adjust the smoothing level)
P(word/class)= (freq of word in given class + α) / (No.of total words in given class+ α*k) [5]

The posterior probability of given sentence using naive bayes is given by
P(class | x1, x2, …, xn) = P(x1|class) * P(x2|class) * ....... * P(xn|class) * P(class) / P(x1, x2, …, xn)
For every sample of test data, we compute the product of class conditional probabilities P(x1|class) * P(x2|class) * ....... * P(xn|class) with the prior probabilities of class P(class). The probability of data p(x1,x2,....,xn) could be computed using marginalization (Here we are substituting the value with 1 as we only need argmax of probabilities).
We use Add-one laplace smoothing when any of the test words are not present in the training data.
Following code perfroms smoothing for words in test data that have zero frequency in training data, performs the product of individual class conditional probabilities, and computes the posterior prabability of sentence given each class.

Assign class label for class with maximum posterior probability among all classes

I am using sklearn.metrics.classification_report for comprehensive performance metrics for multi-class classification
In this part we tune the hyperparameter by training the model with varied hyperparameters from a grid of values for laplace smoothing and pick the best hyperparameter based on performance on validation data. 
The following table shows weighted accuracy results on validation data for a grid search of 'alpha' or 'a' values in laplace smoothing.
Search space = [1000,100,10,1,0.1,0.01,0.001,0.0001]
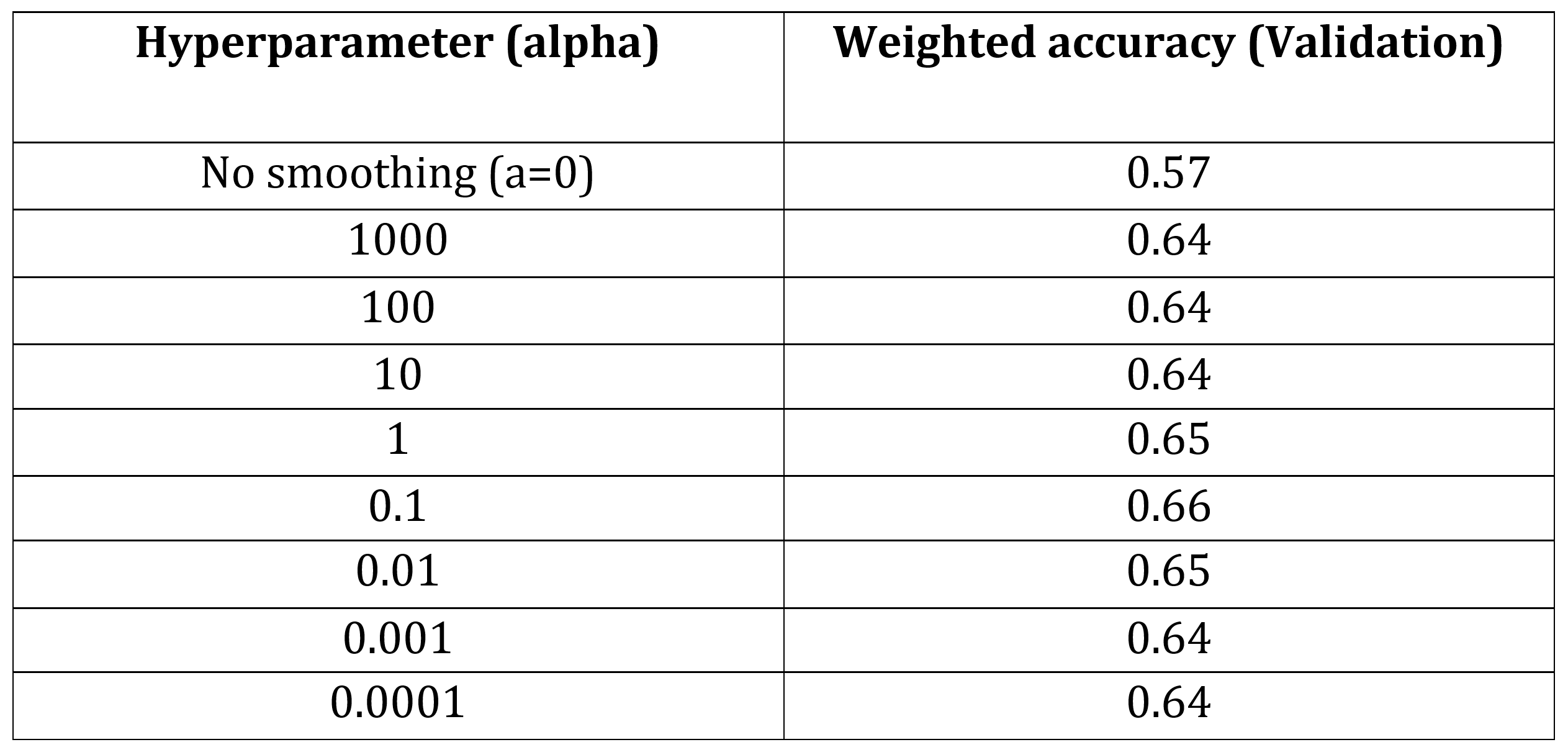
Based on the performance on validation data as shown in the above table, we pick alpha or'a' value as 0.1. We train the model using this value and perform inference on test set for unbiased performance evaluation of the model.

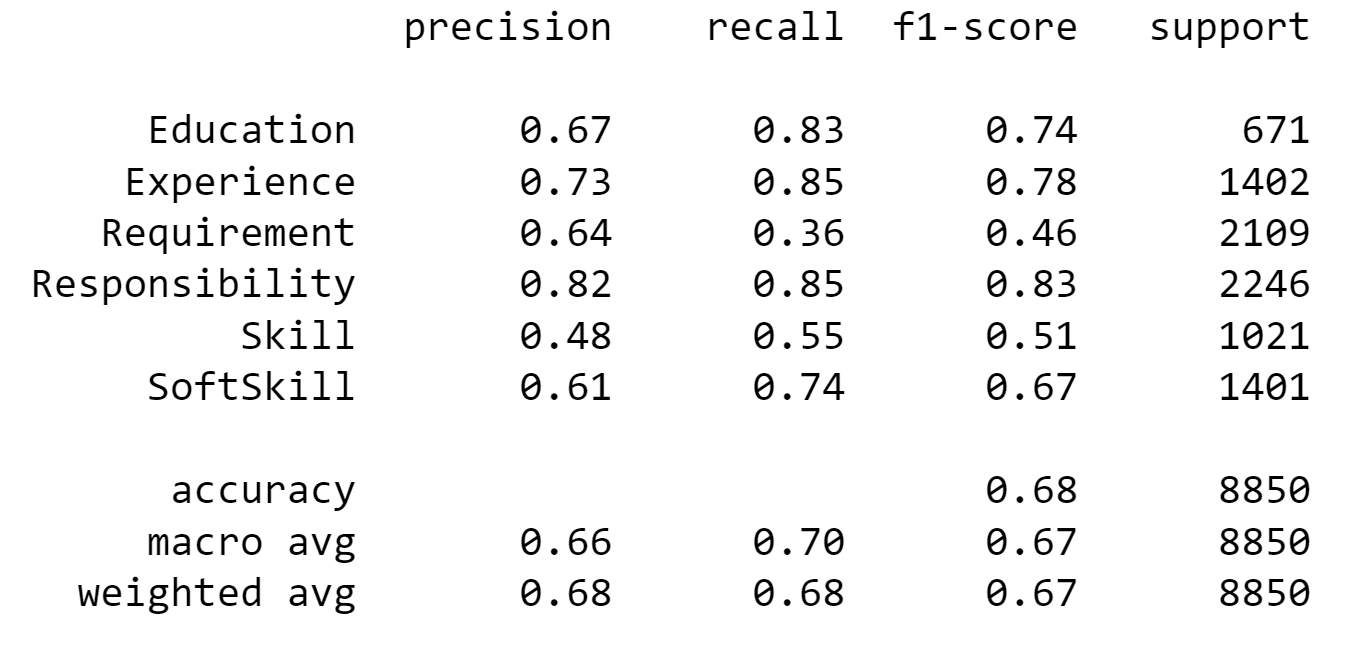
Performance on test set:
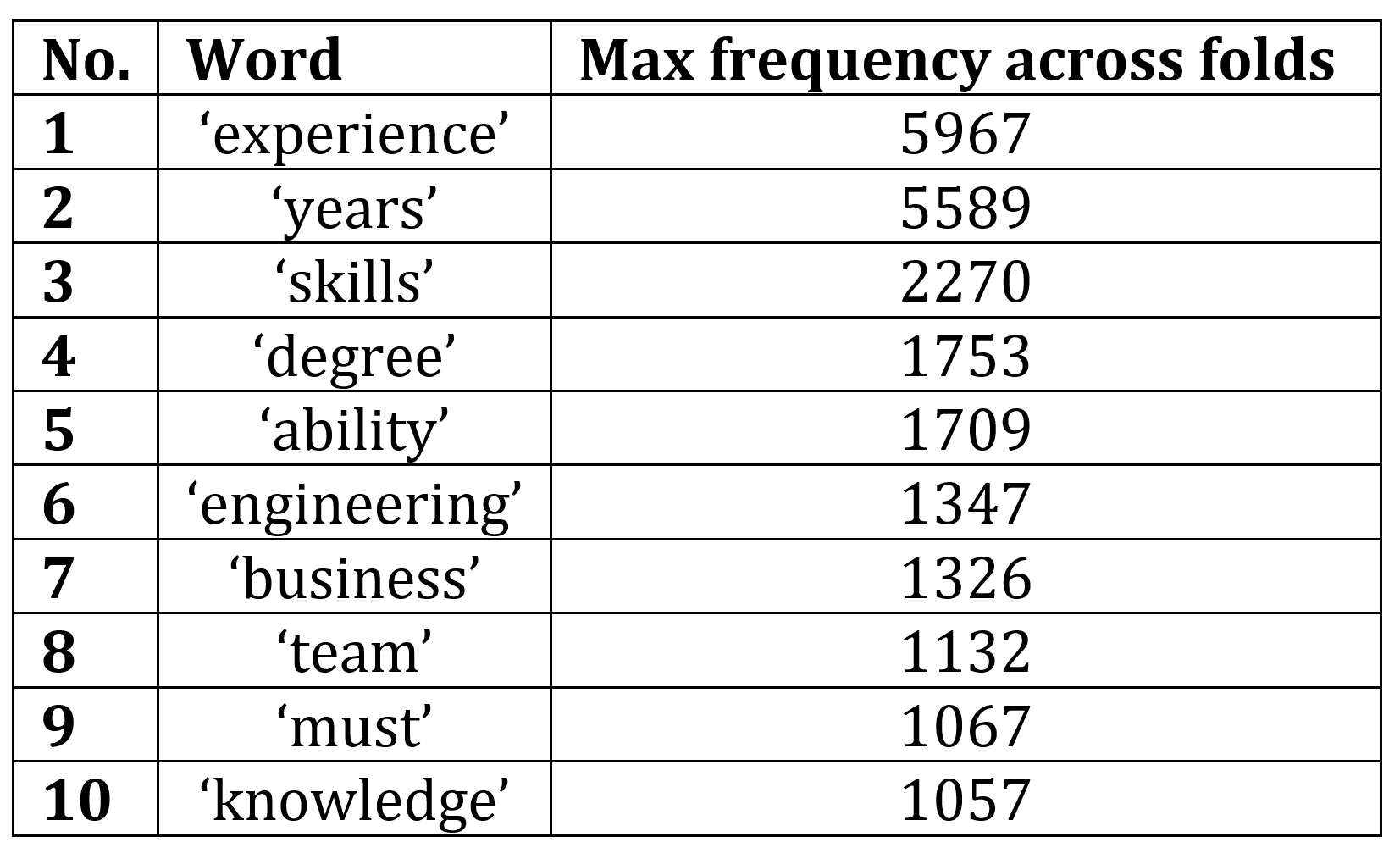
 Experiment 2: Top -10 words that predicts each class
Experiment 2: Top -10 words that predicts each class
We can look at the words with highest probability that predicts each class by identifying the common words with highest probability
This is accomplished using the below code by Identifying common words across all classes, identifying max freq of common words across classes and storing them in a dictionary with word as key and max freq as value. We show top-10 words after sorting the dictionary.

The top-10 words with max freq across folds are:
1. Implemented naive bayes classifier with laplace smoothing from scratch using python without any external libraries and achieved a weighted accuracy score of 67% on test data compared to a baseline weighted accuracy score of 57% without smoothing. (referred tutorial [4])
2. Performed data cleaning by removing punctuation, numbers and stopwords. Created sets of unique words and dictionary of word-frequecy pairs for each class.
3. Implemented laplace smoothing to address 'zero frequency' problem [5]
4. Performed Hyperparameter tuning using grid search of values for 'alpha' in laplace smoothing. Found best performing value of 'alpha' based on validation performance and reported Test performance comprehensively using sklearn.metrics.classification_report.
5. Computed top-10 words that contribute to predictions over all classes using pure python without using any libraries.
Challenge: Initially observed high run times due to nested for loops and not computing dictionary of word frequencies before hand. I tried to implement all computations on the fly at test time.
Solution: This problem can be avoided by pre-computing and storing prior probabilities of classes, conditional class probabilitites of words in dictionary for all classes. This greatly reduces inference time.
Challenge: Lower performance was observed if punctuations, special characters, numerical values are present in the text data
Solution: Closer look revealed the need to remove unnecessary fields like punctuation, special characters and numbers from text data. Removing these has helped increase performance.
Naive Bayes Sentence Classifier from scratch [python]:code
[1] https://www.kaggle.com/datasets/gaveshjain/ford-sentence-classifiaction-dataset?resource=download
[2] https://machinelearningmastery.com/naive-bayes-classifier-scratch-python/
[3] https://shubh-tripathi.medium.com/naive-bayes-classifiers-f897eca83e2c
[5] https://www.analyticsvidhya.com/blog/2017/09/naive-bayes-explained/
created with
Website Builder Software .